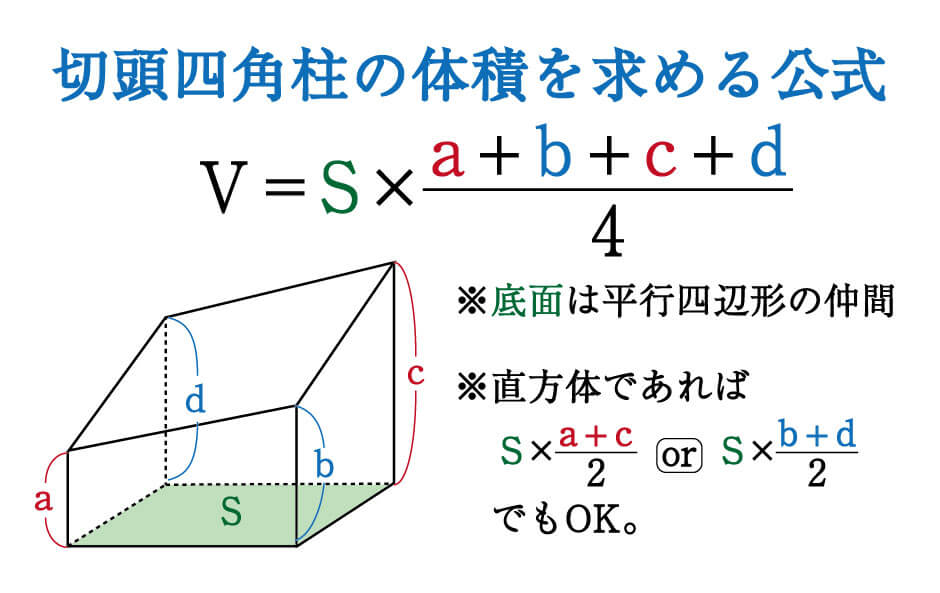
V = 4 3πab2 V = 4 3 π a b 2 ( c c が b b と等しい場合) ふだんからよく使う公式はあまり忘れることはありませんが、たまにしか使わないような公式は忘れやすいです。 立体の体積の公式には、
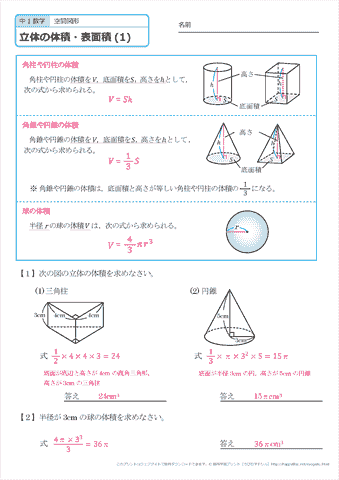
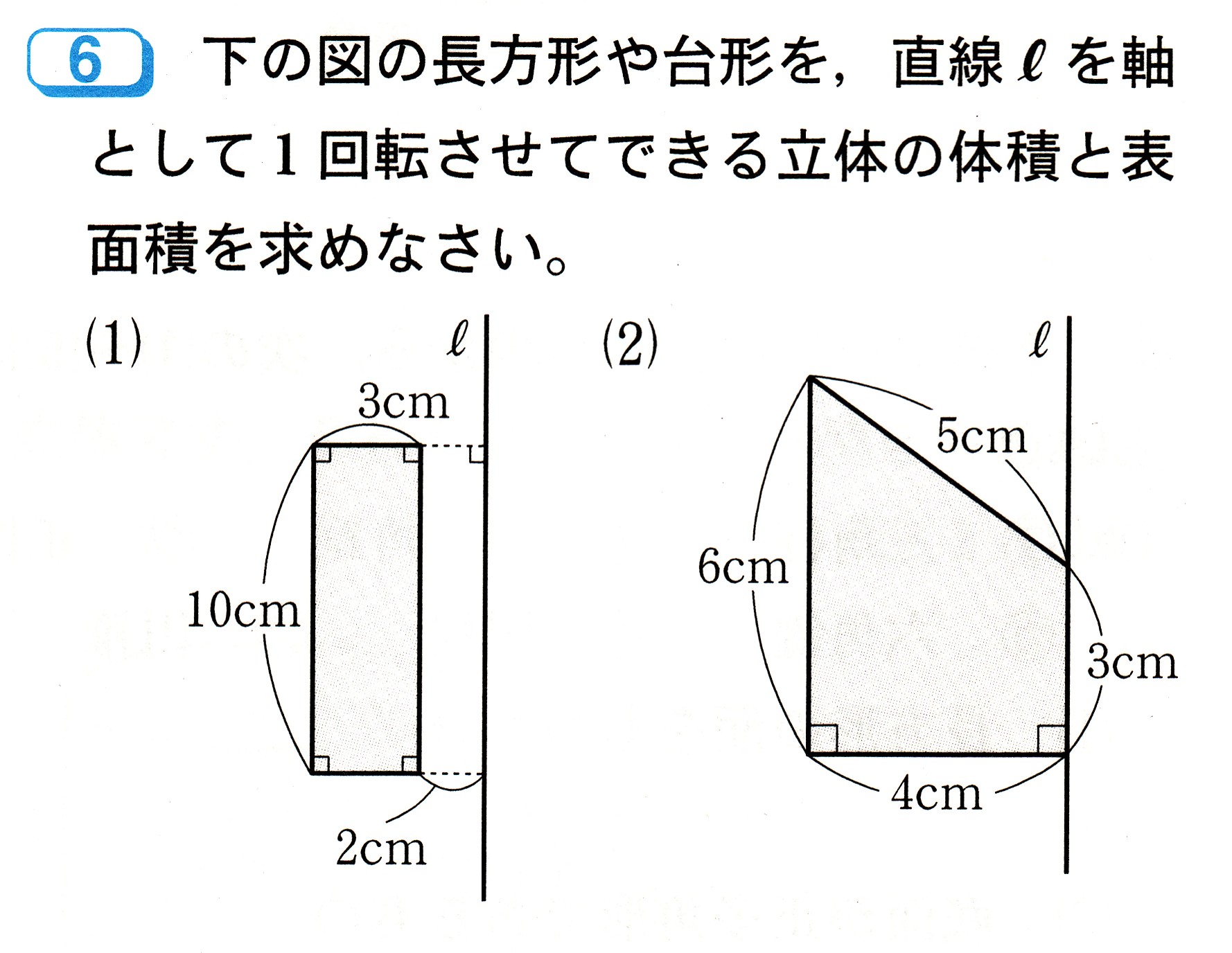
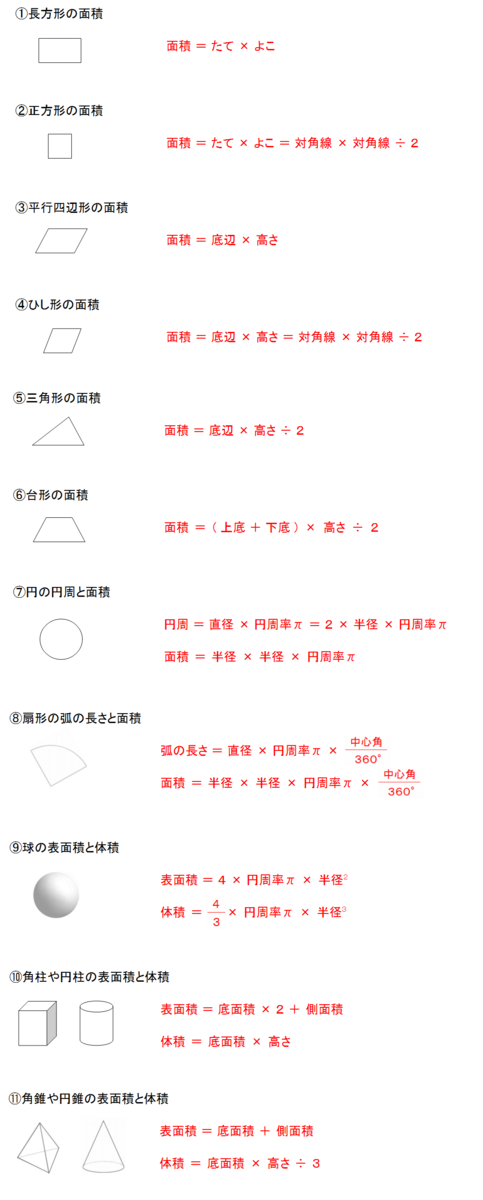
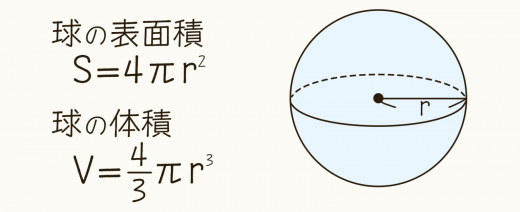
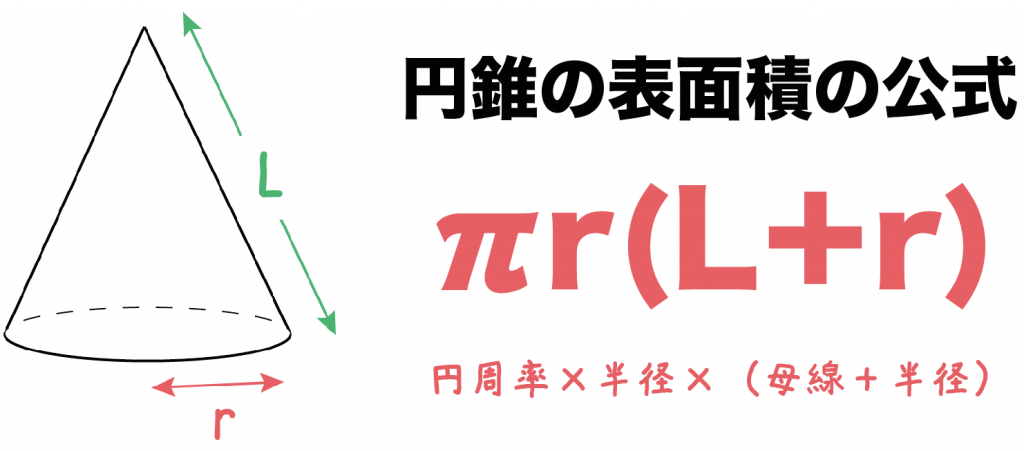
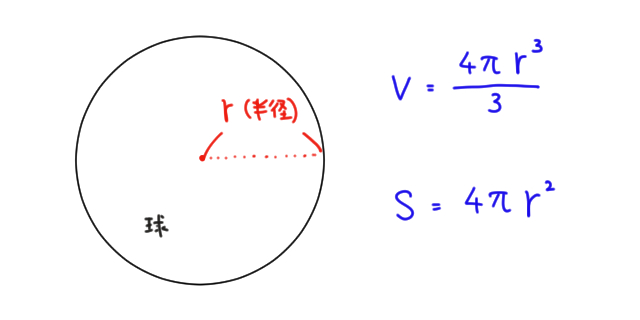
立体の表面積と体積 公式- ある立体の曲面の面積のことを曲面積、もしくは表面積と呼びます。 まずは曲面積の公式をみてみましょう。 2重積分を用いた曲面積(表面積)公式 2変数関数 z = f ( x, y) ≧ 0 で与え球の体積、表面積 半径rの球 表面積=4πr 2 、 体積= 4 3 πr 3 r (例)半径6cmの円 6cm 表面積=4π×6×6=144π(cm 2) 体積= 4 3 π×6×6×6=2π(cm 3) 回転体の体積 回転体は、円錐や円柱、
立体の表面積と体積 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
 |  |  |
「立体の表面積と体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「立体の表面積と体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
 |  | |
「立体の表面積と体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | 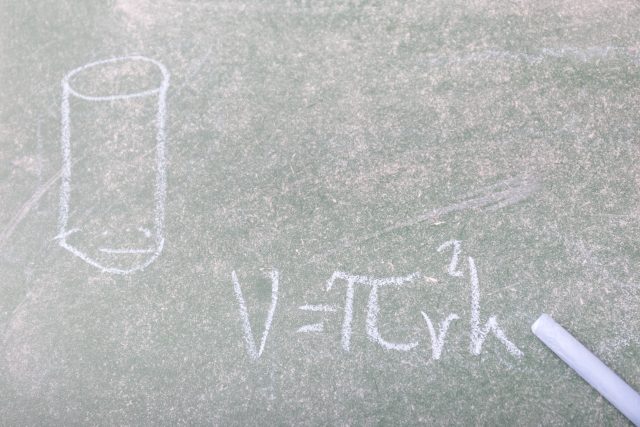 |
 |  |  |
「立体の表面積と体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「立体の表面積と体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  | |
「立体の表面積と体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「立体の表面積と体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  | |
「立体の表面積と体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | 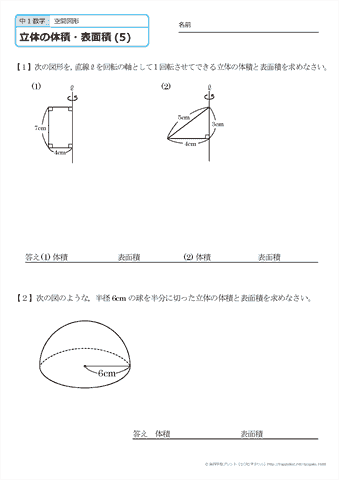 |
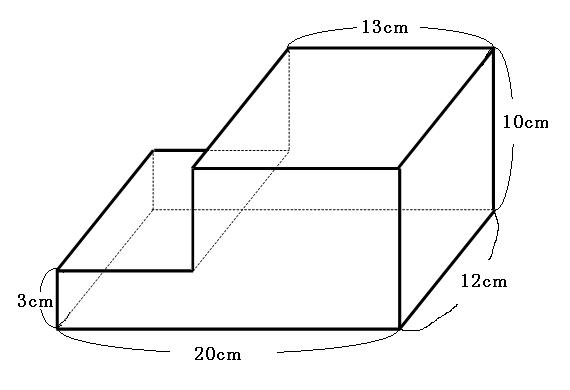
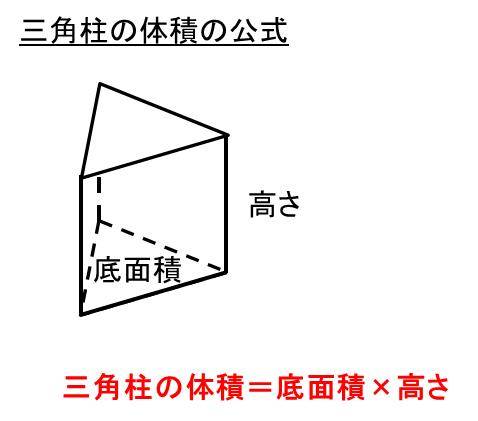
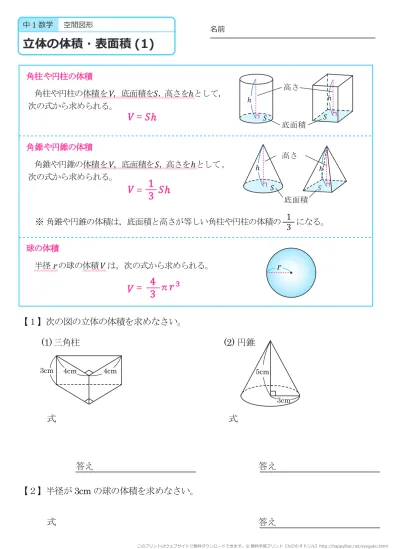
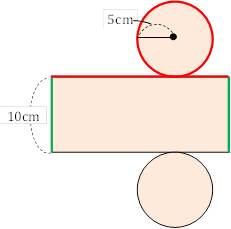
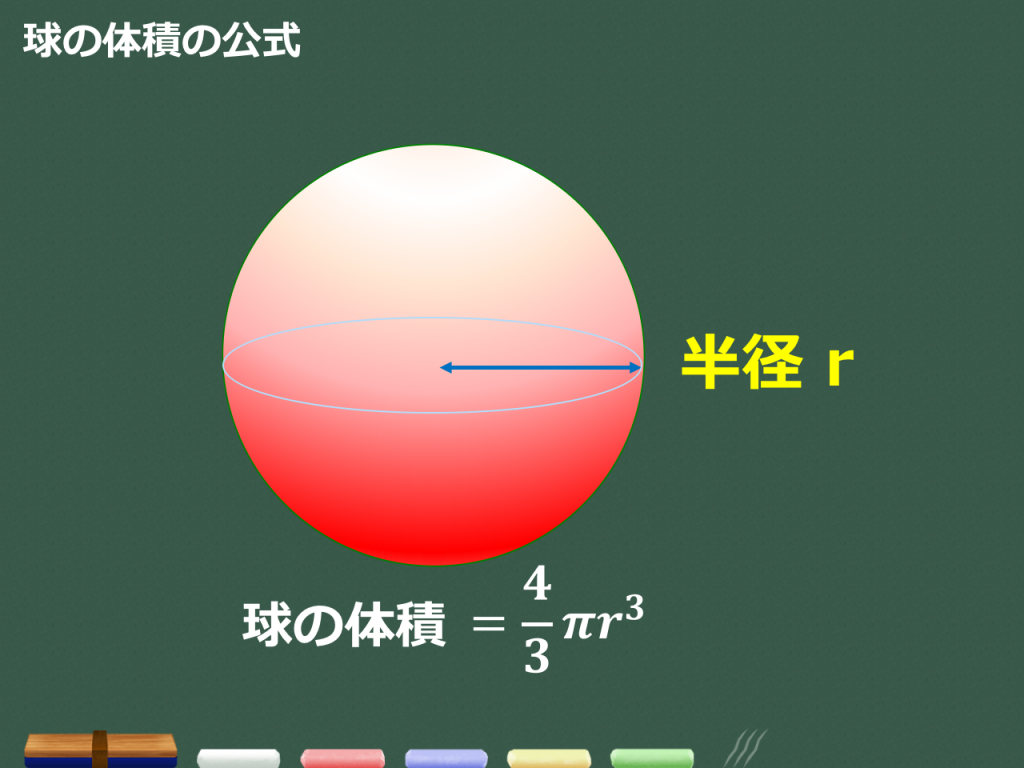
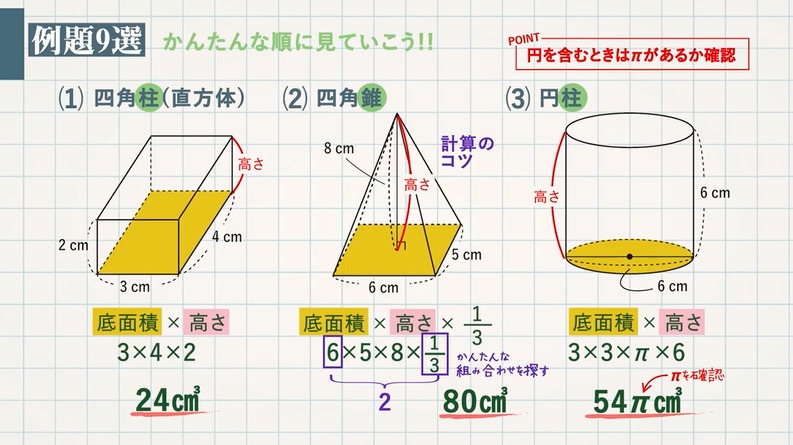
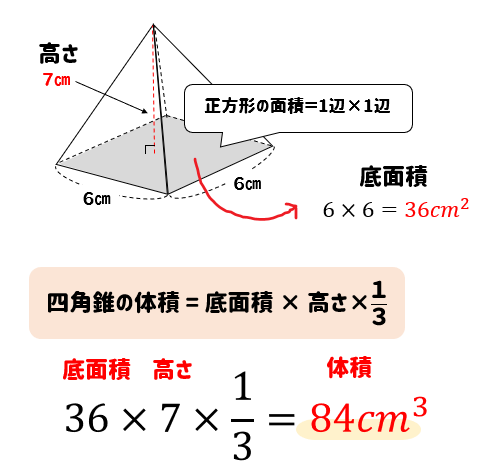
角柱と円柱の体積 = = 底面積× × 高さ 角錐と円錐の体積 = = 底面積× × 高さ× 1 3 × 1 3 球の半径をrとすると、球の体積 = = 4 3πr³ 4 3 π r ³ 意味を理解したら問題を解いてみましょう →球の体積と表面積の公式の覚え方・積分での求め方内の「球の表面積の求め方2」参照。 次は,表面積を計算する公式 S = ∫ x 0 x 1 2 π y 1 y ′ 2 d x S=\displaystyle\int_{x_0}^{x_1}
Incoming Term: 立体の表面積と体積 公式,




0 件のコメント:
コメントを投稿